Four Probability Distributions Every Statistics Student Should Know
If you open up a classical statistics book, you will see endless amounts of information about hypothesis testing, confidence intervals, p-values, etc. Although those topics are important, I have noticed that some people walk away not having a deep understanding of probability distributions (beyond the normal distribution of course). Here are four probability distributions every statistics students should know:
Gaussian distribution
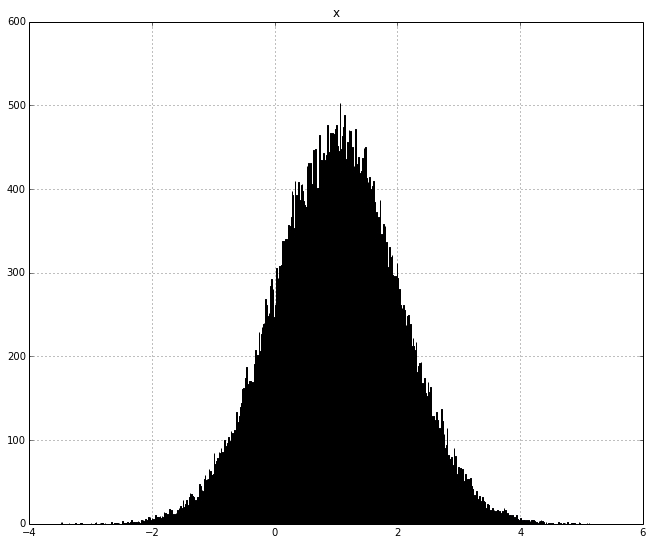
The Gaussian distribution, also known as the normal distribution. It describes the distribution of sum of independent, identically distributed random variables.
Given
And
The T is said to be normally distributed. The average of this sample:
Is also normally distributed, and this is actually more important because the Gaussian distribution describes the distribution of average.
Chi-Squared distribution
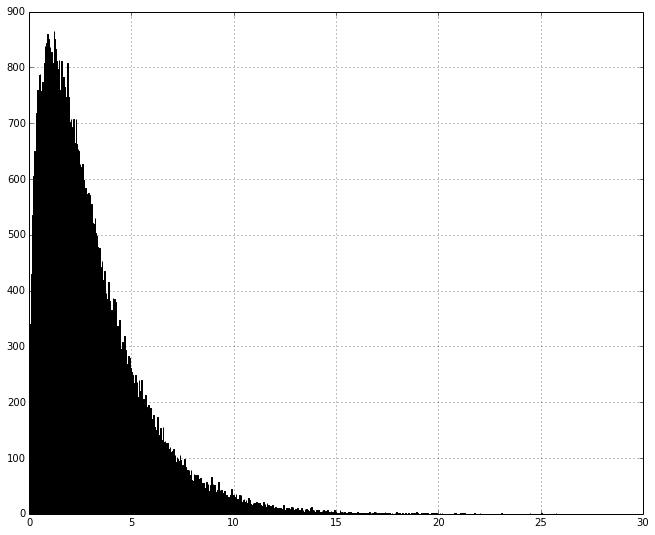
The Chi Squared distribution describes the distribution of squared sums of independent, identically distributed random variables.
Given
And
The T will follow a chi-squared distribution. The reason this is important because the variance is a sum of squares, hence the chi-squared distribution is used to describe the distribution of variances.
The T-distribution
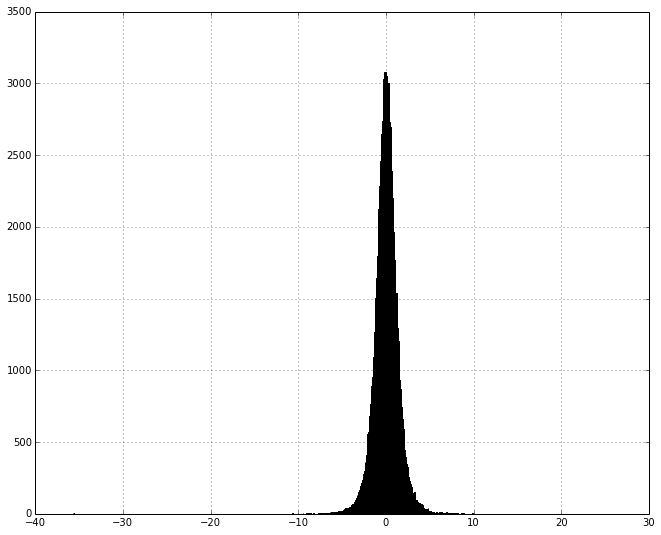
The student t-distribution describes the ratio of a Gauassian random variable with a Chi-Squared random variable. A t-distribution is basically a Gaussain distribution with fatter tails.
Fisher’s F distribution
The F-distribution describes the distribution of the ratio of two chi-squared variables. The is useful if you want to compare two variances against eachother.[1] It is used heavily in Analysis of Variance (ANVOA).